Skip to main content

Solving Van der Pol equation with ivp_solve

Van der Pol’s differential equation is

{d^2x \over dt^2}-\mu(1-x^2){dx \over dt}+x= 0

The equation describes a system with nonlinear damping, the degree of damping given by μ. If μ = 0 the system is linear and undamped, but for positive μ the system is nonlinear and damped. We will plot the phase portrait for the solution to Van der Pol’s equation in Python using SciPy’s new ODE solver ivp_solve.

The function ivp_solve does not solve second-order systems of equations directly. It solves systems of first-order equations, but a second-order differential equation can be recast as a pair of first-order equations by introducing the first derivative as a new variable.

\begin{align*} {dx \over dt} &= y \\ {dy \over dt}&= \mu(1-x^2)y -x \\ \end{align*}

Since y is the derivative of x, the phase portrait is just the plot of (x, y).

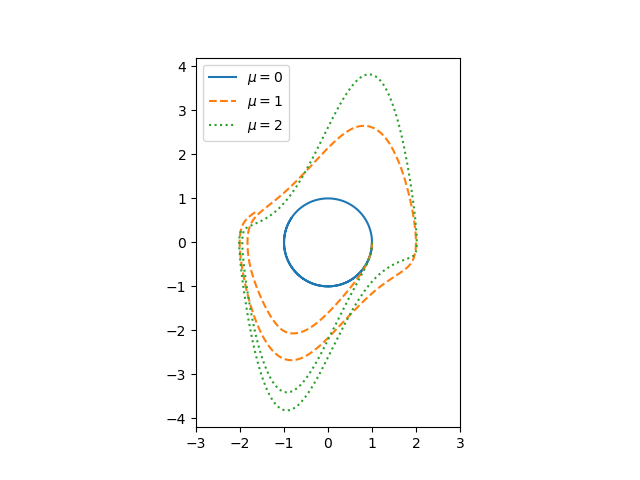
Phase portait of Van der Pol oscillator

If μ = 0, we have a simple harmonic oscillator and the phase portrait is simply a circle. For larger values of μ the solutions enter limiting cycles, but the cycles are more complicated than just circles.

Here’s the Python code that made the plot.

from scipy import linspace
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

def vdp(t, z):
    x, y = z
    return [y, mu*(1 - x**2)*y - x]

a, b = 0, 10

mus = [0, 1, 2]
styles = ["-", "--", ":"]
t = linspace(a, b, 1000)

for mu, style in zip(mus, styles):
    sol = solve_ivp(vdp, [a, b], [1, 0], t_eval=t)
    plt.plot(sol.y[0], sol.y[1], style)
  
# make a little extra horizontal room for legend
plt.xlim([-3,3])    
plt.legend([f"$\mu={m}$" for m in mus])
plt.axes().set_aspect(1)

Related posts



from John D. Cook https://ift.tt/2Q8YgEI
via IFTTT
Labels:

Comments

Post a Comment

Popular posts from this blog

Using RStudio and LaTeX

(This article was first published on r – Experimental Behaviour , and kindly contributed to R-bloggers) This post will explain how to integrate RStudio and LaTeX, especially the inclusion of well-formatted tables and nice-looking graphs and figures produced in RStudio and imported to LaTeX. To follow along you will need RStudio, MS Excel and LaTeX. Using tikzdevice to insert R Graphs into LaTeX I am a very visual thinker. If I want to understand a concept I usually and subconsciously try to visualise it. Therefore, more my PhD I tried to transport a lot of empirical insights by means of  visualization . These range from histograms, or violin plots to show distributions, over bargraphs including error bars to compare means, to interaction- or conditional effects of regression models. For quite a while it was very tedious to include such graphs in LaTeX documents. I tried several ways, like saving them as pdf and then including them in LaTeX as pdf, or any other file ...
Post a Comment
Read more

Explaining models with Triplot, part 1

[This article was first published on R in ResponsibleML on Medium , and kindly contributed to R-bloggers ]. (You can report issue about the content on this page here ) Want to share your content on R-bloggers? click here if you have a blog, or here if you don't. Explaining models with triplot, part 1 tl;dr Explaining black box models built on correlated features may prove difficult and provide misleading results. R package triplot , part of the DrWhy.AI project, is aiming at facilitating the process of explaining the importance of the whole group of variables, thus solving the problem of correlated features. Calculating the importance of explanatory variables is one of the main tasks of explainable artificial intelligence (XAI). There are a lot of tools at our disposal that helps us with that, like Feature Importance or Shapley values, to name a few. All these methods calculate individual feature importance for each variable separately. The problem arises when features used ...
Post a Comment
Read more